A surface normal is an imaginary line which is at right angles to a surface. You can draw a surface normal at any point on a surface.

The angle of incidence (\( \theta_{in} \) in the chapter) is the angle between a ray of light hitting a surface and the surface normal drawn at that point.

\( \theta_{in} \) will be larger than \( \theta_{out} \). Snell's Law says

If \( n_{in}<n_{out} \), then to keep this equation equal, we must have \( \sin{\theta_{in}}>\sin{\theta_{out}} \).

Now, \( \sin{\theta} \) increases as \( \theta \) increases (up to \( 90^\circ \)), so if \( \sin{\theta_{in}}>\sin{\theta_{out}} \), that means \( \theta_{in}>\theta_{out} \)

This is the reverse of the previous question.

\( \theta_{in} \) will be smaller than \( \theta_{out} \). Snell's Law says

If \( n_{in}>n_{out} \), then to keep this equation equal, we must have \( \sin{\theta_{in}}<\sin{\theta_{out}} \).

Now, \( \sin{\theta} \) increases as \( \theta \) increases (up to \( 90^\circ \)), so if \( \sin{\theta_{in}}<\sin{\theta_{out}} \), that means \( \theta_{in}<\theta_{out} \)

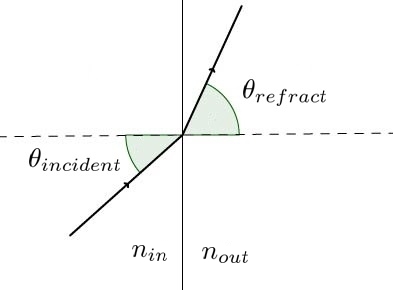
Because \( \theta_{in}<\theta_{out} \), the refractive index to the left must be greater than that to the right, so \( n_{in}>n_{out} \).

• \( n_{in}>n_{out} \); the light ray must be travelling from a more dense to a less dense medium.
• the angle of incidence \( \theta_{in} \) must be greater than the critical angle

It will increase. The critical angle depends on the refractive indices on both sides of the surface.

The critical angle is given by \( \sin{\theta_{crit}}=n_{out}/n_{in} \). If \( n_{out} \) increases, then \( n_{out}/n_{in} \) increases, so \( \sin{\theta_{crit}} \) must increase, and so \( \theta_{crit} \) must increase.

Using Snell's Law \( n_{in}\sin{\theta_{in}}=n_{out}\sin{\theta_{out}} \) we have

• \( n_{in}=1 \) (air)
• \( n_{out}=1.5 \) (glass)
• \( \theta_{in}=34^o \)

So \( 1\times\sin{34^o}=1.5\times\sin{\theta_{out}} \) which gives \( \sin{\theta_{out}}=0.37279... \). Thus \( \theta_{out}=\sin^{-1}{0.37279...} = 21.89^o \) (rounded to 2 dp)

It is \( 65^o \)

• \( n_2 \) is \( n_{in} \)
• \( n_1 \) is \( n_{out} \)
• the radius is measured in a direction opposite to the light, so is negative.

It is positive. In the formula

the numerator (\( n_1-n_2 \)) of the fraction is negative and the denominator ( \( r \)) is negative, so the fraction is positive (negative divided by a negative is positive)

The surface power is

No. In the new light direction, \( n_{in}=1 \) and \( n_{out}=1.5 \) and \( r \) is positive \( 0.25 \), so the fraction is the same.

The surface power is

(rounded to 2 dp)

It increases (gets more negative) because the difference in refractive indices is greater.

One definition is that a convex surface has a positive power and a concave one has a negative power, but that doesn't talk about the shape of the surfaces.

A better definition is as follows:

It is a surface where the radius arrow points in the direction of the higher refractive index. (See Figure 10 in chapter 3 - in the left two surfaces the radius arrow points towards the shaded (higher) refractive index).

The layout of the problem is shown in the diagram below:

The light is travelling left to right, so the negative radius means the centre of the surface is to the left of the surface. The refractive index to the left (1.6) is \( n_{in} \) and the refractive index to the right (1.1) is \( n_{out} \).

To use the paraxial equation we first need the surface power:

(We shouldn't round this power because we need it in further calculations)

The paraxial equation is

Filling in what we know gives

Dividing both sides by \( n_{out}=1.1 \) gives

Hence the image distance is \( 1/V_{out}=0.378 \)m

The apparent depth of the fish is \( 1/1.33\times 20=15.04 \) cm. Note that it isn't necessary here to change everything to metres.

The person's apparent distance is \( 1.33/1\times35=46.55 \) cm