A virtual image is an image that is created by divergent light. It is where the light seems to diverge from, even though it does not really diverge from there.

It diverges the light passing through it. This usually creates a virtual image.

Yes. When the divergence of the light \( V_{in} \) hitting it is more negative than the power \( F \) of the lens. For example, if an object is placed \( -0.2\text{m} \) from a \( +2\text{D} \) lens, then \( V_{in}=1/(-0.2)=-5 \), and so \( V_{out}=-5+2=-3\text{D} \). This divergent light will create a virtual image at a distance of \( 1/(-3)=-0.333\text{m} \)from the lens.

The image also moves closer to the lens. There are a few ways of justifying this:

1. The virtual image from a negative lens is always closer than the object, so when the object moves closer, so must the image.
2. The reason for (1) is because a closer image produces more divergent light, so even more divergent light than that will leave the negative lens, and so this brings the image closer to the lens.

Yes it is possible, although unusual.

If \( V_{in} \) is positive and greater than the lens power, then \( V_{out} \) will also be positive (converging). For example, if \( V_{in}=+5\text{D} \) and \( F=-3\text{D} \), then \( V_{out}=+2\text{D} \). To get a positive value for \( V_{in} \), however, you'd have to create it with a converging lens.

• The virtual image created by a negative lens is closer and smaller than the object.
• The virtual image created by a positive lens is further away and larger than the object.

• A virtual image is created by divergent light leaving a lens. A real image is created by convergent light leaving a lens.
• A virtual image is on the same side of the lens as the object. A real image is on the other side of the lens to the object.
• A virtual image is the same way around as the object. A real image is inverted (upside-down and flipped left-to-right) compared to the object. (You'll have to wait for Chapter 5 to understand why.)
• There are no rays of light at the point of the virtual image. There are rays of light for a real image (badly worded).

You need to use an additional positive lens. If we have an object to the left of a negative lens, the lens will produce divergent light. If we then put a positive lens (with known power) to the right of the negative lens, the divergent light leaving the negative lens hits the positive lens and, if we've placed the positive lens correctly, will be converged to form a real image, as in the picture below:

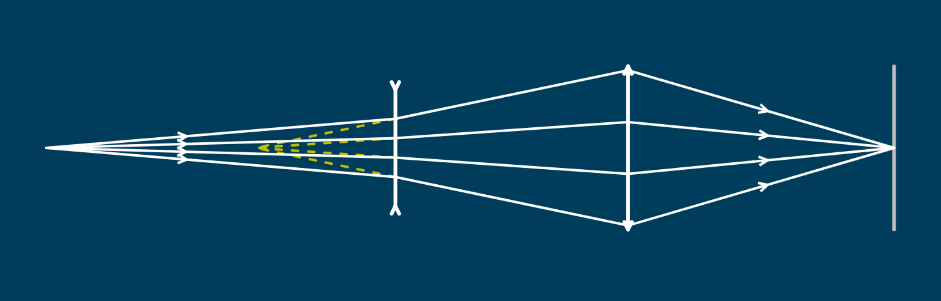
We can work out \( V_{in} \) for the positive lens using the thin lens equation, because we know its power \( F \) and we can measure the image distrance to work out \( V_{out} \).

The object distance \( 1/V_{in} \) is the distance from the positive lens to the virtual image, since that is where the light appears to be diverging from. If we measure the gap between the two lenses, we can work out how far the virtual image is from the negative lens, which is \( 1/V_{out}+(\text{gap length}) \), where the gap length is positive.

It is on the same side as the light entering the lens. If the light is coming from the left, the image focal point is on the left side of the lens.

It depends on which direction the parallel light is travelling. If travelling from left to right, the object focal point is to the right of the lens. If the light is travelling from right to theft, then the definition of the object focal point puts it on the left side of the lens.

So the position of the focal points is contingent on the direction of the light. Luckily, for thin lenses, the focal lengths are always the same even if the names of the focal points change.

Zero.

The virtual image is always closer than the object, and the object can be placed a distance of zero metres from the lens, so in this case the virtual image is also zero metres away.

The vergence entering the lens \( V_{in} \) is \( 1/(-0.4)=-2.5\text{D} \). From the thin lens equation,

The image distance is then \( 1/V_{out}=1/(-6.5) = -0.154\text{m} \) (rounded to 3 decimal places). This is to the left of the lens. It is virtual because it is created by divergent light

All distances must be in metres, so \( 20\text{cm} \) is \( 0.2\text{m} \). The vergence entering the lens \( V_{in} \) is \( 1/(-0.2)=-5\text{D} \). The thin lens equation says

The image distance is then \( 1/V_{out}=1/(-2) = -0.5\text{m} \) (rounded to 3 decimal places). This is to the left of the lens.

In this case, the light is travelling from right (the object) to left (the lens), so rightwardsis the positive direction. This means that the distance from lens to the image on the right is negative.

All distances must be in metres, so \( 90\text{cm} \) is \( 0.9\text{m} \). The vergence entering the lens \( V_{in} \) is \( 1/(-0.9)=-1.111\text{D} \). From the thin lens equation,

The image distance is then \( 1/V_{out}=1/(-6.111) = -0.163\text{m} \) (rounded to 3 decimal places). This is to the right of the lens, and is a virtual image.

The vergence leaving the lens \( V_{out} \) is \( 1/(-0.75)=-1.333\text{D} \). The thin lens equation says

Filling in what we know, we have \( V_{in}-2=-1.333\text{D} \) , so
\( V_{in}=-1.333+2 = -0.666\text{D} \) . The object distance is then
\( 1/V_{in}=1/-0.666 = -1.5\text{m} \) . This is to the left of the lens.

We don't know whether the image is to the left or right of the lens, nor whether it is virtual or real. So we have to try out the various possibilities.

• Suppose the image is real. Then the vergence leaving the lens \( V_{out} \) is positive and equal to \( V_{out}=1/0.25=+4\text{D} \). Using the thin lens equation, \( V_{in}=V_{out}-F=4-3=+1\text{D} \). This is convergent light, so it couldn't possibly come from an object (since an object always produces divergent light). So the image can't be real.

• If the image is virtual, the vergence leaving the lens is \( V_{out}=-4\text{D} \). Using the thin lens equation, \( V_{in}=V_{out}-F=-4-3=-7\text{D} \). Now, we have a divergent \( V_{in} \) so it can come from an object. The object is a distance of \( 1/V_{in}=1/(-7)=-0.143\text{m} \) from the lens.

The object distance is \( -0.45\text{m} \) and the image distance is \( -0.2\text{m} \). The thin lens equation says

Filling in what we know, \( 1/(-0.45)+F = 1/(-0.2) \) , so
\( F=1/(-0.2) - 1/(-0.45) = -7.22\text{D} \).

The object distance is \( -0.3\text{m} \) and the image distance is \( -0.4\text{m} \). The thin lens equation says

Filling in what we know, \( 1/(-0.3)+F = 1/(-0.4) \), so
\( F=1/(-0.4) - 1/(-0.3) = +0.83\text{D} \).