In this figure a point object is placed \( 0.5\text{m} \) to the left of a negative lens with power \( -4\text{D} \) . The distance marked as \( 0.167 \) is discussed in the text.
The lenses discussed in Chapter 1 added convergence to the light passing through them. Not all lenses are like that, however. Some lenses add divergence to the light that passes through them. These lenses have negative power, since divergence is negative. The light leaving a negative powered lens is thus even more divergent than the light entering it (see Figure 1).
In this figure a point object is placed \( 0.5\text{m} \) to the left of a negative lens with power \( -4\text{D} \) . The distance marked as \( 0.167 \) is discussed in the text.
Negative lenses still obey the thin lens equation. For example, suppose there is an object \( 0.5\text{m} \) to the left of a negative lens, as in Figure 1. In Figure 1, the lens has a negative power of, say, \( F=-4{\text{D}} \). Putting these values into the thin lens equation gives
Since \( V_{out} \) is negative, the light leaving this lens is diverging, and it is diverging more than the incoming light \( V_{in} \). The distance from the lens to the image is given by
Since \( V_{out}=-6\text{D} \) in this example, the image should be \( 1/V_{out}=1/(-6)=-0.167\text{m} \) from the lens. This is a negative distance, so the image should be to the left of the lens (because the light in the figure travels from left to right). However, if we look at what is \( 0.167\text{m} \) to the left of the lens in Figure 1, there is absolutely nothing there.
In Chapter 1, images were created by convergent light coming to a point. However, negative lenses typically create divergent light. Another thing that creates divergent light are objects, as we saw in Chapter 1. That suggests a similarity between the divergent light leaving a negative lens and the divergent light coming from an object.
Suppose, as in Figure 2, we see some divergent light, but where it is coming from is hidden. Is the divergent light from a negative lens (as in Figure 1) or is it from an object? Try your luck!
Of course, the game is rigged. The point is, without peeking behind the curtain you can't tell whether the divergent light comes from an object or from a negative lens, and that's what makes the game easy to rig - the computer just draws in the opposite of what you chose before it raises the curtain, and the divergent light doesn't change.
If we can't distinguish these two cases without looking behind the screen, then they are equivalent: that is, the divergent light leaving the negative lens is completely indistinguishable from divergent light leaving an object, even though the causes of the divergent light are quite different.
When the image distance \( 1/V_{out} \) is negative, it isn't where an image actually is; it's where you could put an object to get exactly the same amount of divergent light. In other words, it is where the divergent light leaving the lens seems to be coming from.
This is shown in Figure 3. Just like Figure 1, an object has been placed \( 0.5\text{m} \) from the lens, and divergent light leaves the lens. Some yellow dashed lines have been added, which trace the divergent rays backwards to where they all seem to be coming from.
The fact that this is just like an object can be seen if you click the button marked "Switch". Then, the lens is removed (it remains as a ghost, so you can see where it used to be) and replaced with an object, at just the right place to create the same divergent light. So this object is optically equivalent to the light leaving the negative lens.
You can drag the object to different distances, and \( 1/V_{out} \) is recalculated according to the thin lens equation and marked on the arrow at the bottom.
If you click the button marked "Switch", the picture switches to divergent light coming from an object. Note that nothing changes to the right hand side of where the lens was (which is shown as a faded symbol), so demonstrating again that a virtual image acts more like an object than anything else.
The point where the divergent light leaving the lens seems to come from is called a virtual image. This is a misleading name, but unfortunately it is standard. The reason it is called a virtual image is because the point where the light seems to diverge from is calculated from \( 1/V_{out} \), which usually tells us where the image is. The word virtual indicates that the image doesn't really exist, unlike the images from positive lenses in Chapter 1 (which are called real images).
Although a virtual image doesn't actually exist you can still see it. The virtual image is caused by diverging light leaving the lens, exactly the same as diverging light from a real object, so we can see the virtual image in the same way as we can see any real object. A photograph of a virtual image is shown in Figure 4. The virtual image created by a negative lens is always smaller than the object. Also, from Figure 3, the virtual image is always closer than the object.

This example shows how to use the thin lens equation to work out the position of the virtual image formed by a negative lens. An object is placed 150cm to the left of a negative lens with power \( -7{\text{D}} \). Where does the (virtual) image form?
The sketch for this problem would look something like this:
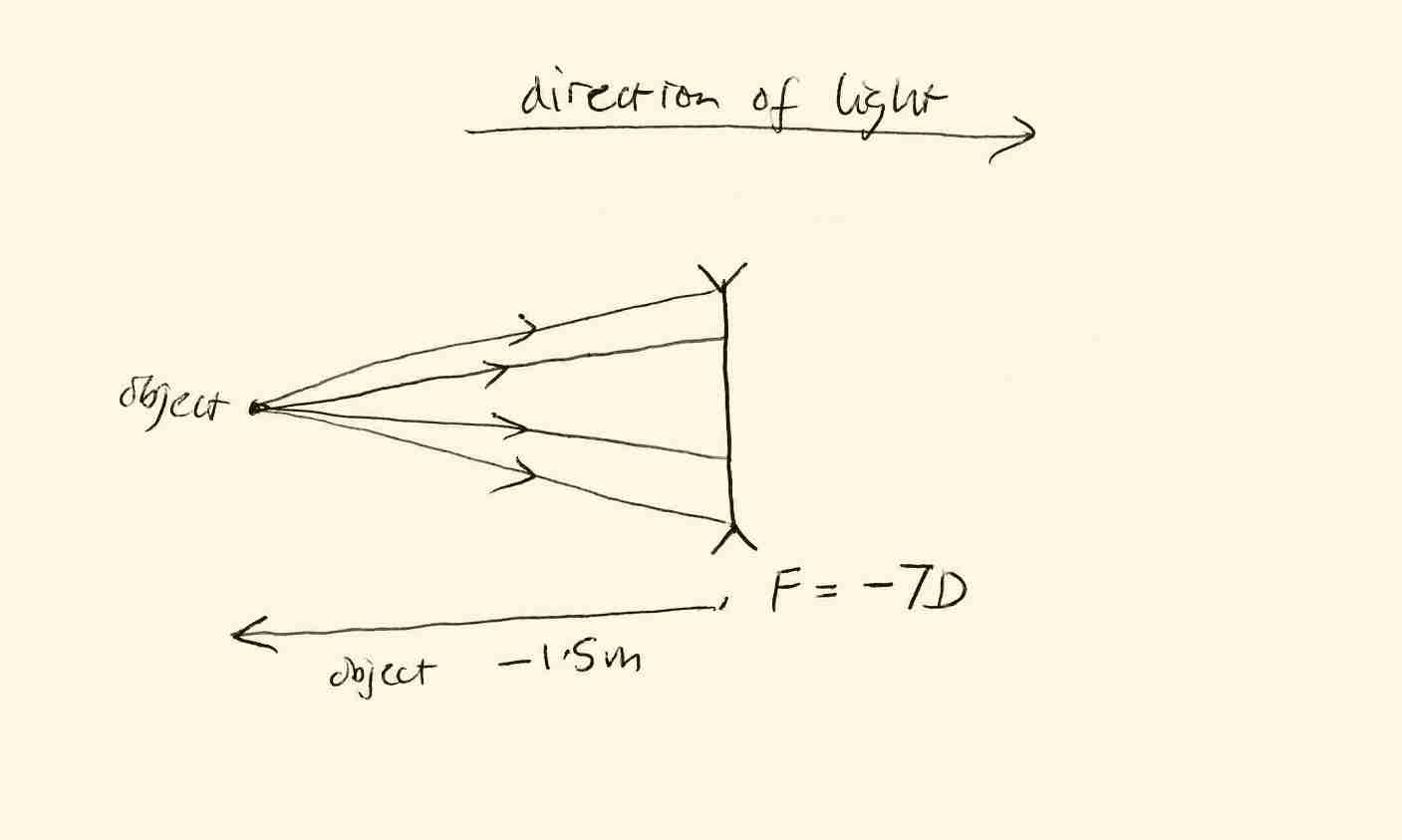
The distance from the lens to the object is negative; so the distance is \( -1.5 \)m. The vergence of the light going into the lens is \( V_{in}=1/(-1.5)=-0.67{\text{D}} \).
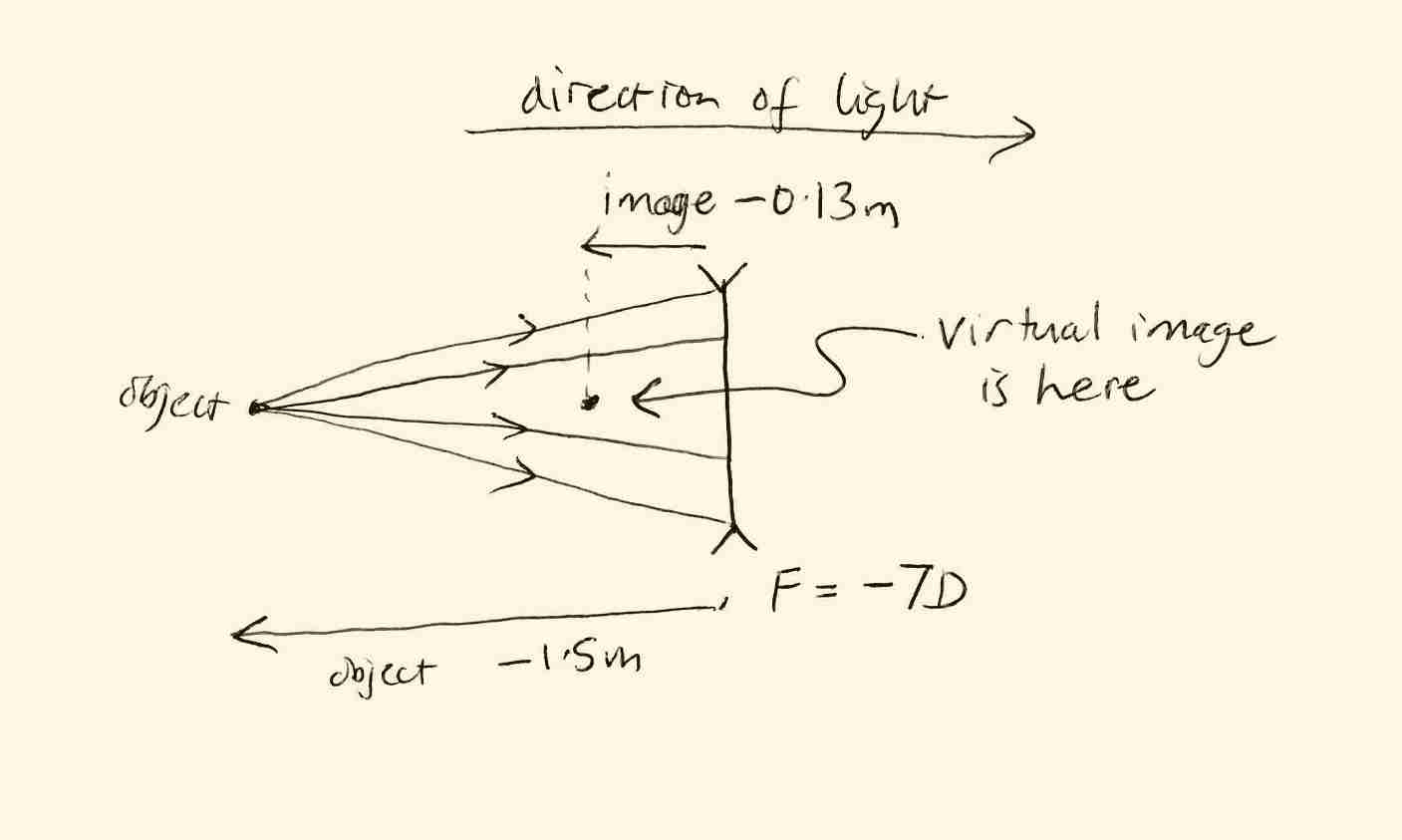
The thin lens equation says \( V_{out}=V_{in}+F \), so \( V_{out}=-0.67+(-7)=-7.67{\text{D}} \).
The "image" forms at a distance of \( 1/V_{out}=1/(-7.67) = -0.13 \)m from the lens. Because it is negative, it is to the left of the lens. So the image forms as in the sketch below:
In Chapter 1, the focal length of a lens was defined as the distance from the lens to the image when parallel light ( \( V_{in}=0 \)) enters the lens. Exactly the same definition can be used with negative lenses, except the focal length will be the distance from the lens to the virtual image. When parallel light with vergence \( V_{in} = 0 \) hits a negative lens with (negative) power 1 \( F \), the vergence of the light leaving the lens \( V_{out} \) is negative. This situation is shown in Figure 5. The vergence of the light leaving the lens is \( V_{out} = F \), as before.
The diverging light \( V_{out} \) leaving the lens seems to be coming from a point which is \( 1/V_{out} \) metres away from the lens (the virtual image). Since \( F=V_{out} \) when \( V_{in}=0 \) , the distance to the virtual image is \( 1/F \), which is the focal length \( f \), which is negative. This is the image focal length .
The object focal length is the distance from lens to object when parallel light leaves the lens; that is, when \( V_{out}=0 \). That means that \( V_{in} + F = 0 \), or \( V_{in} = -F \). Since the value of \( F \) is negative 2, the value of \( -F \) is positive, and so the incoming vergence \( V_{in} \) must be positive. That is, we need to send converging light into a negative lens to make parallel light leave it. This is shown in Figure 6. If you needed to, you could create convergent light by using a positive lens.
The incoming light, with vergence \( V_{in} \), would have converged to a point at a distance of \( 1/V_{in} \) metres to the right of the lens, if the negative lens was not there. The point where the light would have converged to is the object focal point of the negative lens.
It's easy to get the idea that positive lenses always create converging light and negative lenses always create diverging light, but that's a massive oversimplification: it is quite easy to create diverging light with a positive lens. This can be seen in Figure 7. When the object is \( 1\text{m} \) from the lens, convergent light leaves the lens. If you grab the object and move it closer, however, at some point the light leaving the lens becomes divergent. (When that happens, yellow dashed lines are added to show where the light leaving the lens seems to diverge from).
What is going on here? As you move the object closer to the lens, the divergence of the light hitting the lens increases. At some point, it is more divergent than the lens power, and then the lens is no longer able to converge the light completely. The lens still converges the light, just not enough.
Suppose an object is put \( 0.125{\text{m}} \) to the left of a \( +5{\text{D}} \) lens:
The image is formed from divergent light, and so is virtual.
There are two differences between the virtual image created by a positive lens and the virtual image created by a negative lens:

Real images, the kind that we talked about in Chapter 1, are obviously useful. The eye creates a real image of the world on the retina, which is then transmitted to the brain. A camera creates a real image of the world on a CCD or CMOS sensor, which is then stored as an image in memory. Cinema projectors create a real image of the movie data (or film) on a large screen.
What about virtual images? It might seem that virtual images, given that they don't physically exist, are not as useful. However, there are two important uses for virtual images:
Virtual images created by positive lenses are bigger than the object. That is, they magnify the object, so this is useful when the object is small or your eyesight is poor. Magnifying glasses are simply powerful positive lenses, which you hold close enough to the object to create a large virtual image that you can see ( Figure 8). We'll come back to this in a later chapter.
Virtual images created by negative lenses are closer than the object. Myopia is a condition of the eye which means that the person cannot see distant objects clearly, but can see closer objects. A negative lens creates a virtual image that is always closer than the object, and the virtual image is, optically at least, indistinguishable from a real object. By choosing the right negative lens, we can create virtual images of distant objects that are close enough for a myopic person to see them clearly.
Now that you've read this chapter, you can do a self-test