Click the right arrow to show an emmetropic eye, for comparison.
Click the left arrow to show a refractive myope, for comparison.
As we saw in Chapter 8, the eye is built so that the cornea and lens form sharp images of distant objects on the retina, without requiring any accommodation. This state of affairs is called emmetropia (meaning well-proportioned sight). Optically, this means that when parallel light hits the cornea, the light leaving the back of the lens will converge to a point precisely on the retina. If the object is close up, the eye accommodates to focus it.
Not all eyes are like this, however. Some people cannot see distant objects clearly, but they can see closer objects, without needing to accommodate. These people have myopia, meaning short-sightedness. Optically, myopia occurs when parallel light hitting the cornea is converged to a point in front of the retina. By the time the light hits the retina, it has spread out somewhat, and so the image formed on the retina is blurred.
There are two main forms of myopia. The first, called refractive myopia, occurs when the cornea or lens has too much power. For example, the cornea may be curved more than normal, and so have greater power than normal. Then, when parallel light (from a distant object) hits the cornea, it is converged more than it should be. When this light leaves the back surface of the lens, it is still converging too much, and so it comes to a point in front of the retina ( Figure 1).
The second way an eye can be myopic is if it is too long ( Figure 2), which is called axial myopia (from the word axis). In this case, the light leaving the back of the crystalline lens is converging the right amount for a normal-length eyeball, but the retina is actually a little further away than it should be. Thus, the light again converges in front of the retina, at the point where the retina should be. This is the most common form of myopia.
In both axial and refractive myopia, the optical problem is the same: when parallel light hits the cornea, the light leaving the back of the lens is converging too much, so it converges before it arrives at the retina. If we want to form a sharp image on the retina, the vergence of the light leaving the back of the lens needs to be reduced. This will happen if divergent (rather than parallel) light is sent into the myopic eye.
One source of divergent light is objects that are close to the eye. If we bring an object close enough to the myopic eye, it will form a sharp image of that object on the retina ( Figure 3). The point at which an object first becomes clear is called the far point. (The object will also be clear if it is moved even closer than the far point, but in that case the myopic eye is also accommodating. The eye in Figure 3 doesn't do accommodation.)
This is called the far point.
The vergence of light from the far point when it hits the cornea is called the ocular refraction or refractive error, and often is written using the symbol \( K \). For example, if a patient has a far point of \( -0.2\text{m} \), their ocular refraction is \( K = 1/(-0.2)=-5\text{D} \). The eye in Figure 3 has a far point of \( -0.064\text{m} \), so the ocular refraction is about \( -15.6\text{D} \); this would be considered extremely high myopia.
The optical consequence of myopia is blur. If a sharp image of a distant object forms in front of the retina, by the time the light reaches the eye it has spread out again, and the image is no longer sharp. The amount of blur produced by myopia can be calculated using the blur equation introduced in Chapter 5:
The aperture \( a \) in the formula is the pupil diameter, in metres, and \( V_{need} \) and \( V_{out} \) are vergences from the back vertex of the crystalline lens in the eye, when viewing a distant object.
For example, take an axial myope. They have normal optical power, so when they view a distant object, the vergence of the light leaving the back vertex will be the same as for an emmetropic eye; that is, \( 60\text{D} \). However, their retina is further away than an emmetropic retina. The distance from the back vertex to the retina is about \( 16.67\text{mm} \) in an emmetropic eye, so let's give the axial myope a distance of \( 17.5\text{mm} \). Then the vergence (leaving the back vertex) that is needed to form a sharp image at this distance is \( V_{need}=1/0.0175=57.14\text{D} \). If the myope has a pupil diameter of \( a=3\text{mm} \), then the angular blur is
That means anything which is a half degree wide or smaller is blurred out completely.
The difference in vergences \( V_{need}-V_{out} \) is roughly the same as the ocular refraction \( K \). To see this, think of the eye's optics (cornea and lens) as being just a thin lens with a power of \( F=60\text{D} \). If the image screen (the retina) is placed \( 17.5\text{mm} \) away from the thin lens, then (as above) \( V_{need}=57.14\text{D} \) and \( V_{out}=60\text{D} \), so \( V_{need}-V_{out} = -2.86\text{D} \).
From the thin lens equation, a sharp image will be formed when \( V_{in}+F=1/(0.0715)=57.14\text{D} \). Since \( F=60 \) , that means that \( V_{in}=-2.86 \), which is the ocular refraction for this simplified eye. This is the same as \( V_{need}-V_{out} \) for this simplified eye.
Because the ocular refraction is roughly the same as \( |V_{need}-V_{out}| \), and \( |V_{need}-V_{out}| \) determines the amount of blur experienced, we can use blur to estimate refractive error. This is the principle behind the Snellen and Bailie-Lovie eye charts. By seeing what size of letter is blurred beyond recognition we can estimate the size of the blur circle \( \theta_{blur} \), and from that the amount of refractive error. Of course, to do this accurately, we have to measure or control the pupil diameter \( a \), since that also affects the amount of blur.
Anther consequence of the blur equation is that blur worsens when the pupil diameter \( a \) increases. Since the pupil widens at night, many low myopes first discover their condition when trying to read road signs at night.
The myopic eye needs divergent light (equal to their ocular refraction) in order to see clearly. But light from distant objects is parallel, not divergent, so can’t be seen clearly by a myope. However, a myope will be able to see distant objects clearly if we change the vergence of the light to match their ocular refraction when it hits the eye. This can be done with spectacles: that is, a negative lens placed in front of the myopic eye.
Understanding spectacle correction depends on noticing two things:
A myopic eye will see clearly when the light hitting it diverges - or seems to diverge - from the far point.
When light from a distant object (vergence = 0) strikes a negative lens, the light leaving the lens will seem to diverge from the lens’s focal point (Chapter 2).
Suppose we put a negative lens in front of a myopic eye so that the focal point of the lens is at the exactly the same place as the far point of that eye. When light from a distant object passes through the lens, it seems to diverge from the focal point of the lens. However, the focal point is in the same place as the far point. So the light leaving the negative lens also seems to diverge from the far point of the eye. Light diverging from the far point - or seeming to - can be seen clearly by the myope. ( Figure 4).
Clicking the check box inserts a negative lens into the bottom image. The negative lens has a power of \( -20\text{D} \) so it forms a virtual image \( 0.05\text{m} \) to its right (yellow lines). By moving the lens, you can move the point of focus within the eye.
At the right distance, the virtual image created by the spectacle lens is exactly at the far point of the eye. The distance to the virtual image is the sum of the distance from the cornea to the lens and the lens to the focal point (there is a few mm of play in this). This equals the far point distance.
Requiring that the focal point of the negative lens be placed exactly on top of the far point of the myopic eye leads to a simple relationship between the focal length of the spectacles, the far point distance, and the distance from spectacles to the eye. It is this:
The minus sign in front of the spectacle distance is just because the spectacle distance is measured from the spectacles to the right in Figure 4 , and so has a positive sign. The other distances are negative.
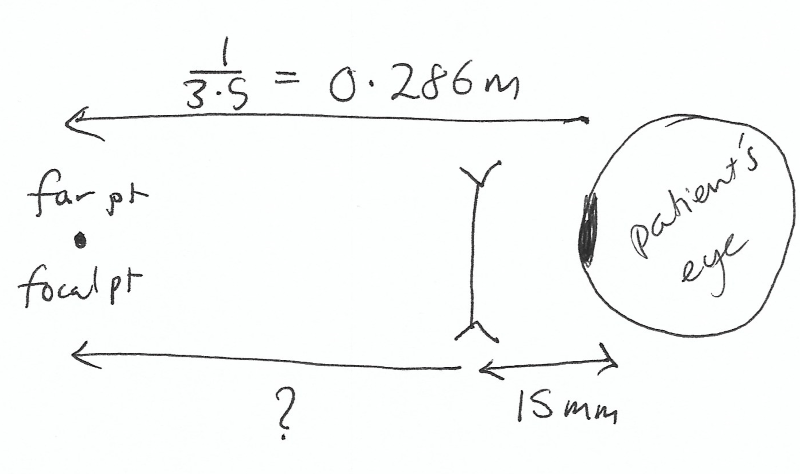
A patient has an ocular refraction of \( -3.5\text{D} \) , and the spectacle distance is \( 15\text{mm} \). What should the power of the spectacles be?
from which \( f_{img}=-0.286 + 0.015 = -0.271\text{m} \) , so the spectacle power is \( 1/(-0.271) = -3.69\text{D} \) . Note that the spectacle power is greater than the ocular refraction. This always happens when correcting myopia with spectacles.
While the sign convention can be quite useful in some contexts, here it is just annoying. The same calculations can be done more easily if you think of all the distances as positive, and then put in the appropriate signs at the end. When doing this, you may need a diagram to keep things straight. Here’s how you could redo Example 1 without the sign convention:
A patient has an ocular refraction of \( -3.5\text{D} \) , and the spectacle distance is \( 15\text{mm} \). What should the power of the spectacles be?
A patient has a pair of spectacles with power of \( -6\text{D} \), worn at a distance of \( 15\text{mm} \). The patient wants to switch to contact lenses. What power should the contacts be?
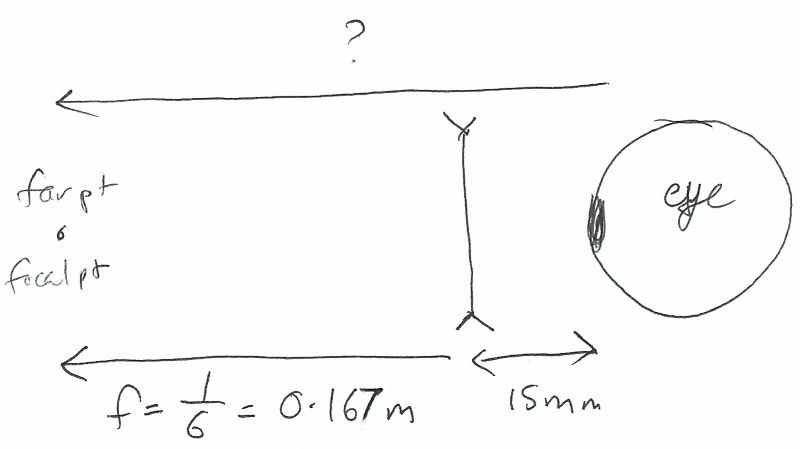
Thus the focal length of the contact lens (which are the “spectacles” in this case) must be \( -0.182\text{m} \), and the power of the contact lens is then \( 1/-0.182 = -5.49\text{D} \). This contact lens has half a dioptre less power than the spectacles. That’s a very noticeable difference, so if you ignored the effect of spectacle distance, you’d have one very annoyed customer.
The relationship between spectacle power and distance can also be worked out using the stepalong formula. Recall from Chapter 4 that with two lenses separated by a gap \( g \), the vergence entering the second lens \( V_{in(2)} \) is given by
To apply this to spectacles, \( V_{out(1)} \) is the vergence leaving the spectacle lens, and \( g \) is the spectacle distance. For a thin lens, \( V_{out(1)} = V_{in(1)}+F \), and when looking at distant objects, this is just \( F \), so
If we think of the eye as the second lens, \( V_{in(2)} \) is the vergence entering the eye. If we want to correct the refractive error, the vergence entering the eye has to be exactly the same as the ocular refraction \( K \), and so, for proper spectacle correction, we must have
If you take the reciprocal of both sides of this equation you get \( 1/K=(1-gF)/F = 1/F - g \). The value \( 1/K \) is the distance to the far point, and \( 1/F \) is the focal length of the spectacles, so this is the same as the spectacle equation given earlier.
In the last chapter, we defined the near point of an emmetrope as the closest distance that an object can be seen clearly. The amplitude of accommodation was just the vergence at the near point. The amplitude of accommodation for myopes is slightly different. The near point of a myope is still the closest distance that an object can be seen clearly, but the vergence at that point isn't the amplitude of accommodation, because we have to take the myope's far point into account.
When an object is placed at the far point, the eye is relaxed, and there is no accommodation. When looking at an object placed at the near point, the eye is fully accommodated, and at its maximum power. The amplitude of accommodation is the difference in the vergence of light from the far point and the vergence at the near point:
For example, a myope who has a far point of 30cm and a near point of 10cm has an amplitude of accommodation equal to
If you ever accidentally swap the near and far points around, you will get a negative value for the amplitude of accommodation. In that case, don't worry, just make it positive.
This definition for the amplitude of accommodation also works for an emmetrope. The emmetrope's far point is at infinity, so the vergence from the far point is zero. Thus, an emmetrope who has a near point of 15cm and a far point at infinity has an amplitude of accommodation equal to
also.
When a myope puts on spectacles, their far and near point change. To distinguish these new points, we say that the artificial far point and the artificial near point are the far point and near point when wearing spectacles. If we’ve done everything correctly, the artificial far point of a myope should be infinity, just like an emmetrope. There is no simple formula for the artificial near point, although you can work it out using the thin lens equation.
One interesting feature of spectacle correction is that if we take an emmetrope and a myope with the same amplitude of accommodation, and then correct the myope, the myope’s artificial near point is closer than the emmetrope’s near point. This effect depends on the spectacle distance and the amount of myopia; a zero spectacle distance (i.e. contact lenses) produces no improvement in the near point. This effect means that a myope wearing spectacles needs to accommodate slightly less than an emmetrope who has the same amplitude of accommodation.
Reading glasses are designed for emmetropes. But what if you have myopia as well as presbyopia? Then, your reading glasses are created by a change in your prescription. The concept is simply that the spectacles myope wears will correct their distance vision, so an myope with spectacles is the same as an emmetrope. We could then put another pair of spectacles on them - the reading glasses - to let them see clearly close up.
This would be silly in practice, so instead we add the power of their distance prescription and the reading glasses together to form a single lens. For example, if a patient had a reading (or working) distance of \( 40\text{cm} \), if they were an emmetrope their reading glasses would have a power of \( +2.5\text{D} \). If that patient was myopic, and their spectacle power was \( -3.5\text{D} \), then putting together their distance prescription \( -3.5\text{D} \) and their reading glasses of \( 2.5\text{D} \), yields a total power of \( -1\text{D} \). That would then be the required power of their reading glasses - still negative, but not as much as their distance prescription.
In this case, the power of the reading glasses (\( +2.5\text{D} \) in the example) is called the near add. It is the power added on top of the distance prescription to allow the patient to see near objects.
Finally, we should note that if a patient is myopic, they may prefer to simply remove their spectacles for near work rather than use reading glasses. This is because removing the negative lens (which is what the myope wears) is the same as adding a positive lens, which is what the near add is.
As mentioned in the last chapter, the success in prescribing the near add depends entirely on how accurate your distance prescription is. If that is wrong (and it frequently is), then a near add calculated from just distances will also be wrong. near adds need to be checked.
Swapping between distance and reading glasses can be quite inconvenient, and many patients prefer to have both distance and reading/near prescriptions built into the same set of spectacles. These spectacles have lenses with at least two powers. A lens with exactly two powers is a bifocal lens, and one with many powers is a multifocal or varifocal lens. We won’t go into the subtleties of the design of these lenses, but will just cover them briefly.
A bifocal lens is a lens with two distinct optical powers, and can be thought of as two lenses which have been cut to fit one another, although they are not manufactured that way. Most of the bifocal lens has the distance prescription power, and a smaller (often D-shaped) segment has the distance power plus the near add. A D-segment bifocal lens is shown in Figure 5. Note that the D segment is displaced towards the nose. This is because the eyes will converge when looking at near objects.
A varifocal lens is one where the power changes progressively from the distance power at the top of the lens to the distance power plus near add at the bottom of the lens. This kind of lens solves the problem shown in Figures 2 and 3 where there is a zone of distances that are not clear either with distance or near prescriptions. Because the varifocal power varies continuously, one can always find a part of the lens with exactly the right power to see an object at any distance.
However, the lens shape that produces this continuous change in power from top to bottom also introduces zones of astigmatism at the sides of the lens. This is diagrammed in Figure 6. Often, the area of the lens free from astigmatism is quite small, and this can be annoying.