Questions for Chapter 4

Here are some questions about the topics in Chapter 4. If you know the answer to a question, great! Click reveal answer to see if you're right. If you don't, have a look back at Chapter 4 to see if you can work out the answer, before you reveal it.

You can click the answer to hide it again.

Two Lens Calculations.

Two thin lenses with powers of \( +6.25\text{D} \) and \( +9.25\text{D} \) are placed \( 84\text{mm} \) apart. An object is placed \( 33.9\text{cm} \) to the left of the first lens. How far is the image from the second lens? Give your answer in metres to 3 decimal places, obeying the sign convention

In this answer, intermediate values are rounded but kept to full decimal places in calculations.

  1. The thin lens equation for the first lens is \( V_{in(1)}+F_1=V_{out(1)} \). We have \( V_{in(1)}=1/(-0.339)=-2.95\text{D} \) , so \( V_{out(1)} = -2.95 +6.25 = 3.3\text{D} \).
  2. Use the stepalong procedure:
    1. The distance of the image from the first lens is \( 1/3.3 = 0.303\text{m} \)
    2. Subtracting the gap gives \( 0.303-0.084=0.219\text{m} \)
    3. One over this is \( 1/0.219 = 4.57\text{D} \), which is \( V_{in(2)} \) for the second lens.
  3. The thin lens equation for the second lens is \( V_{in(2)}+F_2=V_{out(2)} \). From above \( V_{in(2)}=4.57 \), so \( V_{out(2)} = 4.57+9.25 = 13.82\text{D} \)
  4. Finally, the image distance is \( 1/V_{out(2)} = 1/13.82 = 0.072\text{m} \) from the second lens.

Two thin lenses with powers of \( -10\text{D} \) and \( +2\text{D} \) are placed \( 13.9\text{cm} \) apart. An object is placed \( 41.2\text{cm} \) to the left of the first lens. How far is the image from the second lens? Give your answer in metres to 3 dp, obeying the sign convention

In this answer, intermediate values are rounded but kept to full decimal places in calculations.

  1. The thin lens equation for the first lens is \( V_{in(1)}+F_1=V_{out(1)} \). We have \( V_{in(1)}=1/(-0.412)=-2.43\text{D} \) , so \( V_{out(1)} = -2.43 +-10 = -12.43\text{D} \).
  2. Use the stepalong procedure:
    1. The distance of the image from the first lens is \( 1/(-12.43) = -0.080\text{m} \)
    2. Subtracting the gap gives \( -0.080-0.139=-0.219\text{m} \)
    3. One over this is \( 1/(-0.219) = -4.56\text{D} \), which is \( V_{in(2)} \) for the second lens.
  3. The thin lens equation for the second lens is \( V_{in(2)}+F_2=V_{out(2)} \). From above \( V_{in(2)}=-4.56 \), so \( V_{out(2)} = -4.56+2 = -2.56\text{D} \)
  4. Finally, the image distance is \( 1/V_{out(2)} = 1/(-2.56) = -0.391\text{m} \) from the second lens. This is a virtual image.

Two thin lenses with powers of \( +8.25\text{D} \) and \( -2.5\text{D} \) are placed \( 8.8\text{cm} \) apart. An object is placed \( 0.194\text{m} \) to the left of the first lens. How far is the image from the second lens? Give your answer in metres to 3 dp, obeying the sign convention

In this answer, intermediate values are rounded but kept to full decimal places in calculations.

  1. The thin lens equation for the first lens is \( V_{in(1)}+F_1=V_{out(1)} \). We have \( V_{in(1)}=1/(-0.194)=-5.15\text{D} \) , so \( V_{out(1)} = -5.15 +8.25 = 3.1\text{D} \).
  2. Use the stepalong procedure:
    1. The distance of the image from the first lens is \( 1/3.1 = 0.323\text{m} \)
    2. Subtracting the gap gives \( 0.323-0.088=0.235\text{m} \)
    3. One over this is \( 1/0.235 = 4.25\text{D} \), which is \( V_{in(2)} \) for the second lens.
  3. The thin lens equation for the second lens is \( V_{in(2)}+F_2=V_{out(2)} \). From above \( V_{in(2)}=4.25 \), so \( V_{out(2)} = 4.25-2.5 = 1.75\text{D} \)
  4. Finally, the image distance is \( 1/V_{out(2)} = 1/1.75 = 0.570\text{m} \) from the second lens. This is a real image.

The diagram below shows an object placed \( 50\text{cm} \) to the left of a lens with power \( +6\text{D} \). A second lens is placed \( 13\text{cm} \) from the first lens. An image forms \( 300\text{mm} \) to the right of the second lens. What is the power of the second lens (drawn in red) to 2 dp?

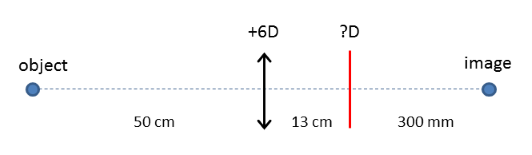
quiz diagram

In this answer, intermediate values are rounded but kept to full decimal places in calculations.

  1. The thin lens equation for the first lens is \( V_{in(1)}+F_1=V_{out(1)} \). We have \( V_{in(1)}=1/(-0.5)=-2\text{D} \), so \( V_{out(1)} = -2 +6 = 4\text{D} \).
  2. Use the stepalong procedure:
    1. The distance of the image from the first lens is \( 1/4 = 0.25\text{m} \)
    2. Subtracting the gap gives \( 0.25-0.13=0.12\text{m} \)
    3. One over this is \( 1/0.12 = 8.333\text{D} \), which is \( V_{in(2)} \) for the second lens.
  3. The image forms \( 0.3\text{m} \) from the second lens, so \( V_{out(2)}=1/0.3 = 3.333\text{D} \) for the second lens.
  4. We know \( V_{in(2)} \) and \( V_{out(2)} \) for the second lens so we can work out its power as \( F_2=V_{out(2)}-V_{in(2)}=3.333-8.333=-5\text{D} \)

Two Surfaces Calculations.

A thick lens with a refractive index of \( 1.5 \) has two surfaces. The first surface has a power of \( +5\text{D} \) and the second surface has a power of \( -1\text{D} \). The lens is \( 15\text{mm} \) thick, and is surrounded by air ( \( n=1 \)). An object is placed \( 0.4\text{m} \) to the left of the first surface. Where does the image form?

In this answer, intermediate values are rounded but kept to full decimal places in calculations.

  1. The paraxial equation for the first lens is \( n_{in}V_{in(1)}+F_{surf(1)}=n_{out}V_{out(1)} \). We have \( V_{in(1)}=1/(-0.4)=-2.5\text{D} \) , \( n_{in}=1 \), \( n_{out}=1.5 \) , and \( F_{surf(1)}=+5 \), so \( V_{out(1)} = (1\times -2.5+5)/1.5 = 1.667\text{D} \).
  2. Use the stepalong procedure:
    1. The distance of the image from the first lens is \( 1/1.667 = 0.6\text{m} \)
    2. Subtracting the gap gives \( 0.6-0.015=0.585\text{m} \)
    3. One over this is \( 1/0.585 = 1.709\text{D} \), which is \( V_{in(2)} \) for the second lens.
  3. The thin lens equation for the second lens is \( n_{in}V_{in(2)}+F_{surf(2)}=n_{out}V_{out(2)} \). From above \( V_{in(2)}=1.709 \), and \( n_{in}=1.5 \), \( n_{out}=1 \), and \( F_{surf(2)}=-1 \), so \( V_{out(2)} = 1.5\times 1.709-1 = 1.56\text{D} \)
  4. Finally, the image distance is \( 1/V_{out(2)} = 1/1.56 = 0.639\text{m} \) from the second lens.

If we ignored the lens thickness, we could think of it as a thin lens with a power of \( 5-1=+4\text{D} \), and then the thin lens equation would say \( V_{in}+F=-2.5+4=1.5 \), so the image would form a distance of \( 1/1.5 = 0.667\text{m} \) from the lens. That's nearly \( 3\text{cm} \) different, but the lens is quite thick.

Lens Shapes.

If the front surface of a lens is convex and the back surface is concave,

  1. what is the lens shape called?
  2. Draw the lens cross-section.

It is a positive meniscus lens.

+meniscus

If both surfaces of a lens are concave,

  1. what is the lens shape called?
  2. Draw the lens cross-section.

It is a biconcave lens.

+meniscus

If the front surface of a lens is convex and the back surface is flat,

  1. what is the lens shape called?
  2. Draw the lens cross-section.

It is a plano-convex lens.

+meniscus

Back Vertex Power (BVP).

Two negative lenses are placed a distance \( d \) apart. Is the BVP

The BVP is negative.

The definition of BVP is the vergence leaving the last lens when parallel light enters the first lens.

  1. If parallel light enters the first lens (\( V_{in(1)}=0 \) ), then divergent light leaves the first lens (\( V_{out(1)}<0 \) ).
  2. As that light travels across the gap between the lenses, it stays divergent.
  3. So the light entering the second lens is divergent (\( V_{in(2)}<0 \)). Since that lens is negative, it diverges the light even more, so \( V_{out(2)}<0 \) as well.

Thus the light leaving the second lens is diverging, and the power (vergence of the light leaving the 2nd lens) is negative.

Two positive lenses are placed a distance \( d \) apart. Is the BVP

It is not possible to say. See the answer to the next two questions.

When will two positive lenses have a positive BVP?

When the powers of the lenses are \( F_1 \) and \( F_2 \), then so long as the gap between the lenses is less than \( 1/F_1 \), or greater than \( (1/F_1+1/F_2) \), the BVP of the two lenses is positive.

Why? We need to consider three cases:

  1. The gap between the lenses is between \( 0 \) and \( 1/F_1 \)
  2. The gap is between \( 1/F_1 \) and \( (1/F_1+1/F_2) \).
  3. The gap is greater than \( 1/F_1+1/F_2 \).

These cases are shown in the picture below (Remember that when working out the BVP, the light entering the first lens is parallel).

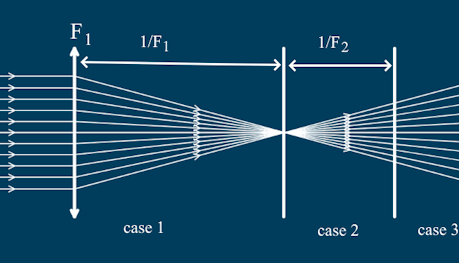
zones

In the first case, the light from lens 1 is always converging, so if we put lens 2 there, the light leaving lens 2 will also be converging, and so the BVP will be positive.

In the second case, the light is diverging from the focal point of the first lens. We can think of this as the same thing as light coming from an object placed at that focal point. If we put the second lens too close to this focal point, it won't converge the light and the BVP will be negative. From chapter 1 we know that too close is less than the focal length \( 1/F_2 \) of the second lens.

In the third case, we are more than \( 1/F_2 \) from the focal point of the first lens, so the divergence of the light is low enough for the second lens to converge it. In that case the light leaving the second lens is convergent, so the BVP is positive.

When will two positive lenses have a negative BVP?

When the powers of the lenses are \( F_1 \) and \( F_2 \), then if gap between the lenses is between \( 1/F_1 \)and \( (1/F_1+1/F_2) \), the BVP of the two lenses is negative.

This is case 2 in the answer to the previous question.

zones

If two positive lenses have a positive BVP, and you move them slightly further apart, what happens to the BVP and why?

It almost always increases. We can look at case 1 and case 3 introduced in the answer to a previous question.

zones

If the second lens is in the area called "case 1" above, then the light hitting it is converging. If we move the second lens further from the first (i.e. to the right), the light entering it will become even more convergent, so the light leaving the second lens will be more convergent. The BVP is the vergence leaving the second lens (when parallel light enters the first) so the BVP increases.

If the second lens is in the area called "case 3" above, then if we move the second lens to the right, the light entering it will be less divergent, and so the light leaving it will be more convergent, so the BVP will again increase.

The only time the BVP won't increase is if we move from case 1 to case 2.

If two negative lenses have a negative BVP, and you move them slightly further apart, what happens to the BVP and why?

It becomes less negative. As the lenses move apart, the divergence entering the second lens gets less, so the divergence leaving it gets less.

Front Vertex Power.

When will two lenses have the same FVP and BVP

When both lenses have the same power.

Two lenses have powers \( F_1=6\text{D} \) & \( F_2=0\text{D} \) & g=0.05m. Work out the front and back vertex powers of this pair of lenses.

The BVP is

\[ BVP = \frac{F_1}{1-dF_1}+F_2 = \frac{6}{1-0.05\times 6}+0 = 8.57\text{D} \]

How is it possible that a zero powered lens makes the BVP greater? It is simply that we are now measuring the power of the system from the place the zero powered lens is put, which is closer to the focus of the first lens than the first lens is itself:

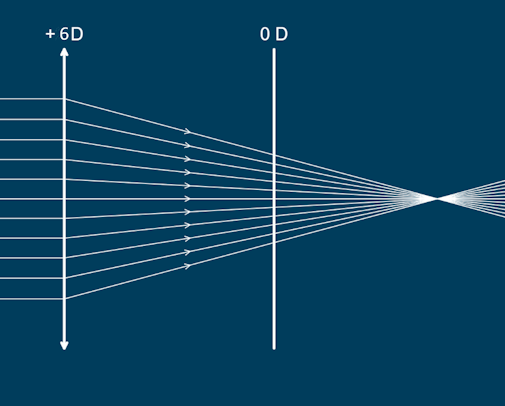
BVP strange

You can see that if you measure the focal length of these two lenses from the second lens, it is shorter, even though the second lens is doing nothing at all to the light.

On the other hand, the FVP is more sensible:

\[ FVP = \frac{F_2}{1-dF_2}+F_1 = \frac{0}{1-0.05\times 0}+6 = 6\text{D} \]

Notice that the zero-powered lens doesn't affect one of these powers.

Back to Chapter 4